Research
Inspired by Feynman’s saying “People who wish to analyze nature without using mathematics must settle for a reduced understanding,” we equally believe that analysis of nature without data must settle for a reduced representation.
This motivates our group to work on bridging the gap between the two.
Climate and Geophysics
Rising sea-levels impact the lives of hundreds of millions of people. Global sea levels are linked to ice sheet dynamics and can be impacted by climate change in many ways. Ice sheets and shelves are slender sheets of non-Newtonian fluid that can flow as a fluid, and bend and break as a solid depending on the timescales of interest. In our group we study the fluid dynamics of ice from two angles: (1) building mathematical models for processes that are currently missing and under-resolved in ice-sheet and climate models and (2) leveraging recent advance in scientific machine learning to expand the scale of data-model comparison.
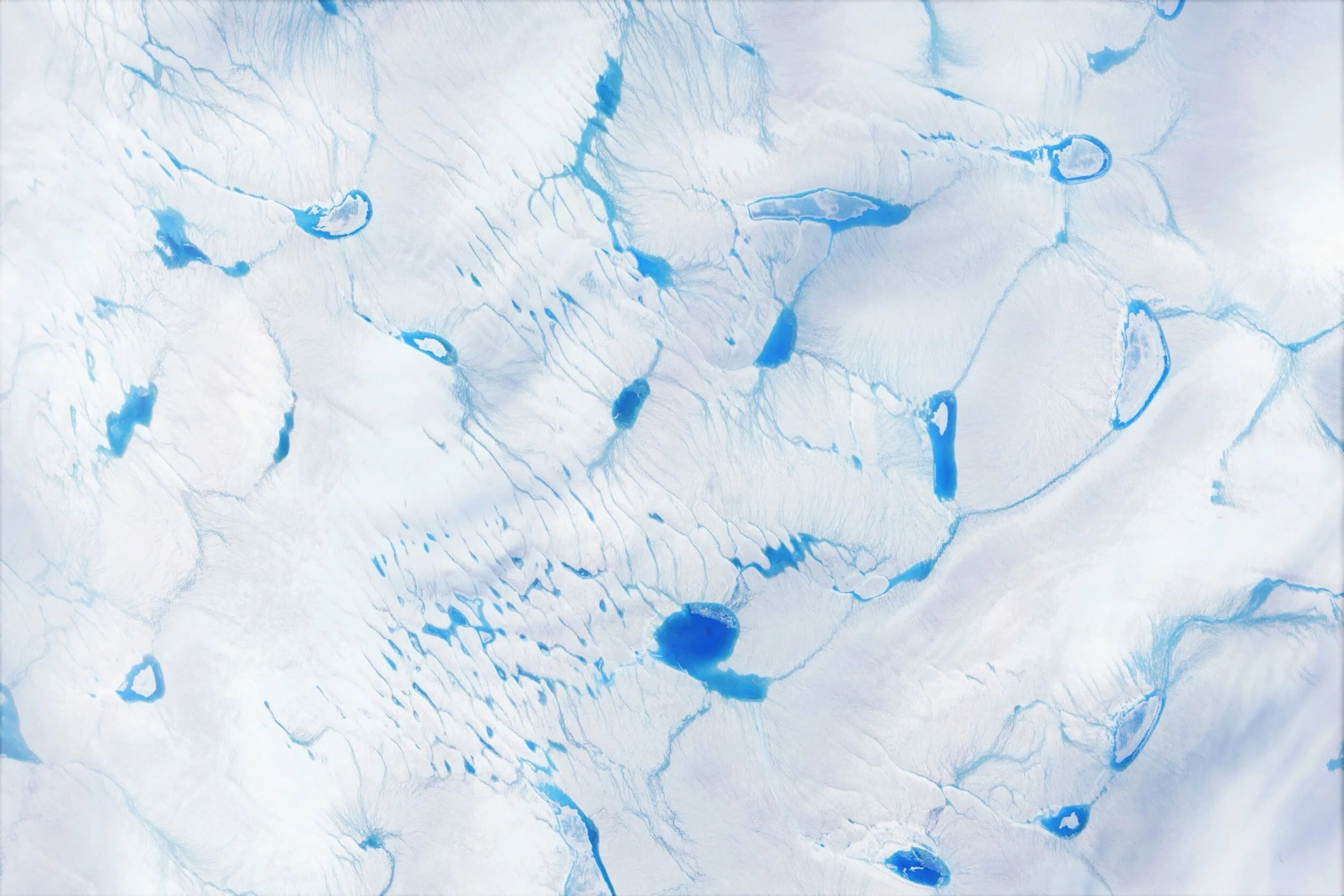
Response of ice-shelf collapse to climate change
Image source: NASA Earth Observatory image by Jesse Allen, using Landsat data from the U.S. Geological Survey
Related papers:
C. Y. Lai, J. Kingslake, M. Wearing, P.-H. Cameron Chen, P. Gentine, H. Li, J. Spergel, J. M. van Wessem, “Vulnerability of Antarctica’s ice shelves to meltwater-driven fracture," Nature, 584, 574–578 (2020). doi: 10.1038/s41586-020-2627-8
A major open question affecting future sea levels is whether meltwater-driven fracturing on ice shelves will significantly impact the future loss of the Antarctic Ice Sheet. Atmospheric warming threatens to accelerate the retreat of the Antarctic Ice Sheet by increasing surface melting and facilitating hydrofracturing, where meltwater flows into and enlarges fractures on ice shelves, potentially triggering ice-shelf collapse and acceleration of sea-level rise. Here we used an innovative combination of theory and deep-learning to develop the stability diagram for Antarctic fractures. We find that large portions of Antarctic ice shelves will be energetically favorable to unstable hydrofracture, and the collapse of these regions would trigger significant acceleration of ice flow.
Many unanswered questions are to be explored, such as the processes governing the catastrophic collapse of ice shelves, and how the complex rheology impacts the breaking of thin sheets of ice. In the future we hope to couple our new hydrofracture model with ice-sheet models to improve predictions of Antarctica's response to atmospheric warming and contributions to sea-level rise. Water flows under the ice sheets
Surface meltwater reaches the ice-sheet base through fractures and forms a network of water flows beneath the ice sheet. After a surface lake drains, the water body at the ice-bed interface transiently deforms the overlying ice sheet. Then the surface deflection relaxes over time as the water drains through the subglacial water network (right figures). This water network at the base of ice sheets lubricates the ice bed. Understanding how a warming climate will affect the water networks running under ice sheets is vital for predicting ice-sheet dynamics, yet the hydrological structure beneath the ice sheets remains poorly constrained by observations due to difficulties in accessing the deep ice bed.
Here we develop a novel method to determine the transmissivity of subglacial water networks that uses a mathematical model to describe the relaxation dynamics of ice sheet over a permeable substrate. We compared the model with a lab experiment and field data (GPS uplift data) and show that transmissivity can increase by up to two orders of magnitude throughout the melt season.
Related papers:
C. Y. Lai, L. A. Stevens, D. L. Chase, T. T. Creyts, M. D. Behn, S. B. Das, H. A. Stone, “Hydraulic transmissivity inferred from ice-sheet relaxation following Greenland supraglacial lake drainages," Nat. Commun., 12, 3955 (2021). doi.org/10.1038/s41467-021-24186-6
Melwater forms lakes over the Greenland Ice Sheet.
NASA Earth Observatory image by Jesse Allen, using EO-1 ALI data provided courtesy of the NASA EO-1 team and Landsat data from the U.S. Geological Survey.
“If nature were not beautiful it would not be worth knowing, and life would not be worth living.”
— Henri Poincaré (1908)
Scientific Machine Learning
Recent advances in deep learning are transforming our ability to solve problems in physical and mathematical sciences. These advancements enable us to process and interpret vast and ever-expanding datasets. We are interested in applying deep learning to both observational and computational datasets to (1) use physical principals to improve the machine-learning predictions, (2) use machine learning predictions to help understand the physics, and (3) inspire new science questions and discoveries in climate science and fluid dynamics that would be otherwise difficult. Beyond predicting existing knowledge, we aim to leverage deep learning to inspire new insights in the realm of mathematical and physical sciences.
Searching singularity formation in fluids with deep learning
In mathematical fluid dynamics, a challenging question persists regarding whether an inviscid incompressible fluid with initially smooth velocity and finite energy, governed by the 3-dimensional Euler equations, can develop singularities within a finite time. This problem has been unsettled for close to a century and is closely related to one of the seven Millennium Prize Problems. Here physics-informed deep learning allows us to numerically find the first smooth asymptotic self-similar blow-up profile of the 3D Euler equations for the Luo-Hou scenario, or equivalently, the self-similar blow-up solution of the 2D Boussinesq equation. This is the first use of deep learning to identify a self-similar blowup solution.
Furthermore, our method discovered the first example of an unstable self-similar solution that was previously impossible! This shows exciting promises to use this method to discover unstable solutions for other fluid equations.
Our work was featured in this Quanta magazine article.Related papers:
Y. Wang, C. Y. Lai, J. Gomez-Serrano, T. Buckmaster, “Asymptotic self-similar blow-up profile for 3-D axisymmetric Euler equations using neural networks," Phys. Rev. Lett., 130, 244002 (2023). doi.org/10.1103/PhysRevLett.130.244002
Image credit: “watercolor painting of vortex in fluids background in white” by DALL-E 2
Deep learning constrained by physical laws
Neural networks can be trained on simulations to emulate the behaviors of fluid flows, or more generally systems described by a set of partial differential equations. This approach has a range of benefits, from less computational expense compared with direct numerical simulations, inverse problems, to discovering new behaviours beyond predictions of known physics. In our group we study ways to combine supervised or unsupervised deep learning models with robust physical laws to discover patterns hidden in large-scale data.Related papers:
Y. Wang, C. Y. Lai, “Multi-stage neural networks: Function approximator of machine precision,” J. Comput. Phys., 2024, 112865 (2024). doi.org/10.48550/arXiv.2307.08934
R. Eusebi, G. A. Vecchi, C. Y. Lai, M. Tong, “Realistic tropical cyclone wind and pressure fields can be reconstructed from sparse data using deep learning,” Nature Commun. Earth Environ., 5, 8 (2024). doi.org/10.1038/s43247-023-01144-2
Y. Iwasaki, C. Y. Lai, “1D ice shelf hardness inversion: Clustering behavior and collocation resampling in physics-informed neural networks,” J. Comput. Phys., 492, 112435 (2023). https://doi.org/10.1016/j.jcp.2023.112435
Y. Wang, C. Y. Lai, David J. Prior, C. Cowen-Breen, “Deep learning the flow law of Antarctic Ice Shelves,” submitted. https://doi.org/10.21203/rs.3.rs-2135795/v1
R. Eusebi, G. A. Vecchi, C. Y. Lai, M. Tong, “Realistic tropical cyclone wind and pressure fields can be reconstructed from sparse data using deep learning,” Nature Commun. Earth Environ., 5, 8 (2024). doi.org/10.1038/s43247-023-01144-2
Y. Iwasaki, C. Y. Lai, “1D ice shelf hardness inversion: Clustering behavior and collocation resampling in physics-informed neural networks,” J. Comput. Phys., 492, 112435 (2023). https://doi.org/10.1016/j.jcp.2023.112435
Y. Wang, C. Y. Lai, David J. Prior, C. Cowen-Breen, “Deep learning the flow law of Antarctic Ice Shelves,” submitted. https://doi.org/10.21203/rs.3.rs-2135795/v1
First deep learning-based continent-wide Antarctic feature detection
Antarctica fractures impact ice flow and are a major obstacle to polar fieldwork, but a continent-wide ice shelf map of fractures was not available. This also hinders continent-scale comparison between model and observations. For the first time we trained a deep neural network, the U-Net, to identify ice-shelf fractures on satellite imagery (125m/pixel), yielding the first continent-wide map of Antarctic fracture features. Related papers:
C. Y. Lai, J. Kingslake, M. Wearing, P.-H. Cameron Chen, P. Gentine, H. Li, J. Spergel, J. M. van Wessem, “Vulnerability of Antarctica’s ice shelves to meltwater-driven fracture," Nature, 584, 574–578 (2020). doi: 10.1038/s41586-020-2627-8
Deep learning-based fracture detection (Greenland)
A video by PhD student Josh Rines illustrating the training of a deep convolutional neural network for Greenland fracture detection!Fluids and Soft Matter
The interaction between fluid flows and solid structures, e.g. fluid-structure interactions, occurs in many important applications in geophysics, climate, biomedicine, and energy technologies. For example, when fluid flows through a deformable structure the material softness impacts the flow patterns and the flow can reshape the deformable structure. In both nature and technology, the fluid-fluid and fluid-solid interfaces often trigger unexpected and nonlinear phenomena. In our group we aim to understand the laws governing such behaviors and their relevance in real-world applications.
Bubble bursting: universal cavity and jet dynamics
Related papers:
C. Y. Lai, J. Eggers, and L. Deike, “Bubble bursting: universal cavity and jet profiles," Phys. Rev. Lett., 121, 144501 (2018). doi: 10.1103/PhysRevLett.121.144501
Bubbles bursting is ubiquitous in everyday life and is important for the climate. After a bubble bursts, a jet forms, breaks, and emits water droplets to the atmosphere. Over the ocean, the aerosol drops generated by bubble bursting stay in the atmosphere due to their small size (ranges from 1 to 100 μm), and they affect Earth’s radiation balance, cloud and ice crystal formation, and precipitation and threaten human health by sending marine biotoxins and viruses into the atmosphere.
It has been challenging to experimentally resolve the interfacial dynamics at the scale of a few microns to centimeters. Here, combining theory and direct numerical simulations (using the Gerris Flow Solver) that resolved the multi-scale flow physics, we studied the interplay between inertia, surface tension and viscous forces. We developed an analytic expression that describes the full history of the jetting process, from cavity collapse to droplet formation.Relaxation of bubbly flows in slender channels and cracks
When densely packed air bubbles in liquid water jam, the bulk media can gain rigidity and behave as a solid, even though air and water themselves are fluids! Densely packed bubbles, e.g. foams, exhibit many interesting behaviors and are involved in a wide range of applications, including fire-fighting, energy storage using compressed foams, and enhanced oil recovery. Here we study how jammed and compressed bubbles relax through slender channels.
Inspired by foam fracturing, a technology to reduce freshwater use in fracking and minimize the creation of wastewater, we developed a system for injecting aqueous foam instead of water to fracture a brittle solid matrix. We discovered unexpected fracture-propagation dynamics governed by the compressibility of bubbles in foam. We are also interested in understanding other systems involving injection of compressible two-phase flows in porous environments. Related papers:
C. Y. Lai, B. Rallabandi, A. Perazzo, Z. Zheng, S. Smiddy, and H. A. Stone “Foam-driven fracture," Proc. Natl. Acad. Sci., 201808068 (2018). doi: 10.1073/pnas.1808068115
Fluid-driven cracks in gels
The interplay of fluids and cracks is ubiquitous in nature and technology: examples include magma intrusion into Earth’s crust, hydraulic fracturing, and Greenland rapid lake drainages. It is difficult to measure crack propagation and determine fluid pathways kilometers below the surface. Here we designed an idealized laboratory experiment to study the propagation and closure of fluid-filled cracks in a transparent hydrogel matrix. We developed scaling arguments and mathematical models to understand how a viscous fluid cracks an elastic matrix during fluid injection, and subsequently, how elastic relaxation of the solid forces the fluid to flow backwards (e.g. backflow) during crack closure. The time-dependent crack shapes were visualized using fluorescent dyes. In the figure below the fluid is shown in yellow and the unfractured hydrogel in shown in blue. This image method allowed us to demonstrate the universal dimensionless crack shapes that reveal the self-similar dynamics during the cracking and backflow process.
Related papers:
C. Y. Lai, Z. Zheng, E. Dressaire, G. Ramon, H. E. Huppert, H. A. Stone, “Elastic relaxation of fluid-driven cracks and the resulting backflow," Phys. Rev. Lett., 117, 268001 (2016). doi: 10.1103/PhysRevLett.117.268001
C. Y. Lai, Z. Zheng, E. Dressaire, H. A. Stone, “Fluid-driven crack in an elastic matrix in the toughness-dominated limit," Philos. Trans. R. Soc. A, 374, 20150425 (2016). doi: 10.1098/rsta.2015.0425
C. Y. Lai, Z. Zheng, E. Dressaire, J. Wexler, H. A. Stone, “Experimental study on penny-shaped fluid-driven cracks in an elastic matrix," Proc. R. Soc. A, 471, 20150255 (2015). doi: 10.1098/rspa.2015.0255